Lectures and Workshops

Complex numbers and their use in geometry - Jurij Kovič

We will explain basic concepts related to complex numbers. We will answer questions like: What are complex numbers, why do we call them so, how were they discovered, how we perform arithmetic operations on them, and where do we use them? Particular attention will be given to the use of complex numbers in geometry.

 

 

 

Statistics and probability in daily life - Lara Lusa

Statistics and probability are present in everyone’s daily life, even though few might realise it. Statistics is the science of collecting, presenting, analysing and interpreting data. (Descriptive) statistics is used to summarise available data and make them easily understandable and accessible; birth and mortality data, disease statistics, unemployment data and economic growth data are just some examples where statistics summaries are necessary. Very sophisticated statistical (inferential) models and complex data collection methods can be used to make predictions about future events or explain phenomena: who will win the next elections, what is the weather going to be tomorrow, is it safe to a launch a space shuttle, is the performance of a soccer player going to be good next season?
Some knowledge of statistics and probability enhances our understanding of the word. Can you develop a strategy that will help you win the lottery or other luck games? (The answer is, in most cases, no!) How worried should you be about the result of a medical test that indicates the presence of a rare disease? (Not too worried, in some circumstances!) Should you believe that the inhabitants of your little neighbouring town are the smartest in your country, since the news reported that it had the highest proportion of students that graduated with honours? (Again, they might not as smart as the statistics suggest.) The lecture will present these and other real data examples where it is useful to understand statistics, and introduce basic statistical principles.

 

Happy ending problem - István Kovács

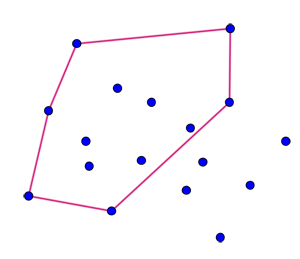Imagine that we are given 5 points in the plane so that no three of them lie on the same line. Do there exist at least four points among them, which form the vertices of a convex quadrilateral? The answer is yes, and such four points can be found by looking at the convex polygon induced by the given five points. In 1933, Eszter Klein posed the following generalization: let n be a positive integer, n ≥ 3. Does there exist a number N(n) such that in an arbitrary set of at least N(n) points in the plane with no three lying on the same line, one can always find n points, which form the vertices of a convex n-gon? For instance, the previous exercise shows that N(4) = 5.
In 1935, Pál Erdös and György Szekeres proved that such a number N(n) exists for each integer n ≥ 3. The story led to the marriage of Klein and Szekeres in 1937, and because of this Erdös named Klein’s problem “happy ending problem”. The number N(n) attracts attention of mathematicians still in these days. Short time before his death in 1996 Erdös wrote the following: “I would certainly pay 500$ for a proof that N(n) = 2^(n−2) + 1 for all integers n ≥ 3”.

 

Non-platonic polyhedra - Russ Woodroofe

A platonic polyhedron is a polyhedron where every face is a regular polygon, all the faces are congruent to one another, and the same number of faces meet at every vertex. You likely have been told that the only platonic polyhedra are the (regular) tetrahedron, cube, octahedron, dodecahedron, and icosahedron. You may even have seen a proof of this fact.
In this session, we'll focus instead on the polyhedra that are not platonic. Can you find a polyhedron with 10 vertices, 19 edges, and 11 faces? How, or why not? Can you find a polyhedron with a square face and a pentagonal face? We'll show both how to construct new examples, and why there are no examples with certain combinations of properties.

 

 

Shortest distance on surfaces - Jasna Prezelj

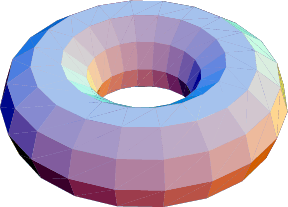The problem of finding the shortest distance on a given surface is a well known one. We all know that on a plane the shortest distance between two points is the line connecting them. But finding the shortest distance on an uneven terrain quickly becomes difficult. Let us say we are looking for the shortest distance between two towns in Slovenia (and let us say we can swim across any river and climb any mountain.). We will try to find the shortest path over uneven platonic bodies and some other surfaces that we can easily describe and model.

 

 

Q.E.D. - Štefko Miklavič

Q.E.D. is an abbreviation for the Latin expression "quod erat demonstrandum", meaning "what was to be shown". The phrase or its abbreviated form is often used at the end of mathematical proofs, where the correctness of a certain mathematical statement is proven. One example of it is the well known Pytaghoras' Theorem, which states that in every right triangle  the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides. But do we know how to prove that this always holds?  During the lecture we will take a look at some of the well-known mathematical statements and through them discover different methods of proofs.