Predavanja in delavnice

Kompleksna števila in njihova uporaba v geometriji - Jurij Kovič

Obdelali bomo osnovne pojme povezane s kompleksnimi števili. Odgovorili bomo na vprašanja, kot so: Kaj so kompleksna števila, zakaj jih tako imenujemo, kako so bila odkrita, kako računamo z njimi in kje vse jih uporabljamo? Še posebej veliko pozornosti bomo posvetili uporabi kompleksnih števil v geometriji.

 

 

 

Statistika in verjetnost v vsakdanjem življenju - Lara Lusa

Statistika in verjetnost sta prisotni v vsakdanjem življenju vsakega posameznika, čeprav se le redko kateri tega zavedajo. Statistika je veda, ki se ukvarja z zbiranjem, analizo in interpretacijo podatkov.
(Opisna) statistika povzame podatke z namenom, da postanejo kompleksni podatki čim bolj preprosto razumljivi in dostopni; podatki o rojstvih in smrti prebivalcev, o boleznih, o nezaposlenosti in gospodarski rasti so le nekateri primeri, kjer so statistični povzetki potrebni. Napredne statistične (inferenčne) metode in kompleksni načini zbiranja podatkov lahko prispevajo k napovedi dogodkov ali k razlagi raznih pojavov: kdo bo zmagal na volitvah, kakšno bo vreme jutri, ali bo vzlet vesoljskega letala varen, kakšna bo uspešnost nekega nogometaša v naslednji sezoni?
Poznati osnove statistike in verjetnosti pomaga bolje razumeti svet okrog nas. Ali lahko izumite strategijo, s katero boste zmagali na
loteriji ali pri kakšni drugi igri na srečo? (Odgovor je ne, v veliki večini primerov!) Koliko je smiselno biti zaskrbljen zaradi
pozitivnega rezultata diagnostičnega testa, ki nakaže, da imate redko bolezen? (Ne preveč zaskrbljen, v nekaterih primerih!) Ali so
prebivalci sosednje male vasi najpametnejši, saj imajo največji delež zlatih maturantov? (Morda niso tako pametni, kot kažejo statistike.) Predavanje bo predstavilo te in druge primere, ki temeljijo na resničnih podatkih in kjer je razumevanje statistike uporabno, ter uvedlo temeljne statistične koncepte.

 

Problem s srečnim koncem - István Kovács

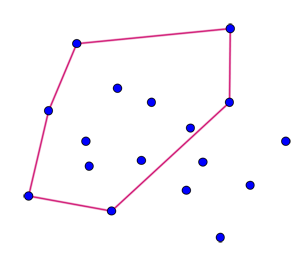Zamislite si, da imamo pet točk v ravnini, tako da nobene tri ne ležijo na isti premici. Ali izmed teh petih točk vselej obstajajo štiri, ki tvorijo oglišča konveksnega štirikotnika? Odgovor je da, in take štiri točke lahko najdemo tako, da pogledamo konveksni poligon, generiran s petimi točkami. Leta 1933 je Eszter Klein zastavila naslednjo posplošitev zgornje naloge: Naj bo
n celo število, več je ali enako 3. Ali obstaja tako število N(n), da med poljubno množico vsaj N(n) točk v ravnini, pri čemer nobene tri ne ležijo na isti premici, vedno lahko najdemo n točk, ki tvorijo oglišča konveksnega n-kotnika? Prejšnja naloga nam na primer pokaže, da je N(4) = 5.

Leta 1935 sta Pál Erdös and György Szekeres dokazala, da število N(n) obstaja za vsako celo število n, večje ali enako 3. Zgodba se je končala s poroko med Kleinovo in Szekeresom leta 1937, in zaradi tega je Erdös Kleinin problem poimenoval “problem s srečnim koncem” (“happy ending problem”). Števila N(n) pa zanimajo matematike tudi dandanes. Malo pred svojo smrtjo leta 1996 je Erdös zapisal: “I would certainly pay 500$ for a proof that N(n) =2^(n−2) + 1 for all integers n ≥ 3”.

 

Neplatonski poliedri - Russ Woodroofe

Platonski polieder je polieder, kjer so vse ploskve regularni poligoni, vse ploskve so med seboj kongruentne in v vsaki točki se sreča enako število ploskev. Verjetno ste slišali, da naj bi bili edini platonski poliedri (regularen) tetraeder, kocka, oktaeder, dodekaeder in ikozaeder. Morda ste videli celo dokaz.
Tu bomo govorili o poliedrih, ki niso platonski. Lahko najdete polieder z 10 točkami, 19 robovi in 11 ploskvami? Kako, oziroma zakaj ne? Lahko najdete polieder s kvadratno in pentagonalno ploskvijo? Pokazali bomo tako konsturkcije novih primerov, kot tudi zakaj v nekaterih primerih takšni poliedri ne obstajajo.

 

Najkrajše razdalje na ploskvah - Jasna Prezelj

Problem iskanja najkrajše razdalje na dani ploskvi je naokoli že zelo dolgo. Vsi vemo, da je na ravnini najkrajša razdalja med dvema točkama dana z ravno črto, ki ju povezuje. Če pa poskusimo najti najkrajšo razdaljo na kaki neravni ploskvi, pa to ni več tako enostavno - recimo, če iščemo najkrajšo pot med dvema krajema v Sloveniji (in privzamemo, da lahko prebrodimo vse reke in preplezamo vse gore kjerkoli). Najti bomo poskusili najkrajše poti na površinah platonskih teles ter še na nekaterih drugih ploskvah, ki se jih da dovolj preprosto opisati ali modelirati.

 

 

Q.E.D. - Štefko Miklavič

Q.E.D. je okrajšava za latinski izraz "quod erat demonstrandum", ki pomeni "kar je bilo potrebno pokazati (demonstrirati)". Fraza oz. okrajšava zanjo se tradicionalno postavlja na konec matematičnih dokazov, v katerih je demonstrirana pravilnost določene (matematične) trditve. Primer take trditve je nam vsem dobro poznani Pitagorov izrek, ki trdi, da je v vsakem pravokotnem trikotniku vsota kvadratov dolžin katet tega trikotnika enaka kvadratu dolžine hipotenuze. Pa znamo tudi dokazati, da je to vedno res? V predavanju si bomo ogledali dokaze nekaterih najbolj znanih matematičnih trditev, ter preko njih spoznali različne vrste dokazov.